What is the best hand in poker? The absolutely best hand in pokeris the Royal Flush, which is made of Ace, King, Queen, Jack, and Ten, and all of those must be the same suit. For Example, Ah Kh Qh Jh Th would make a Royal Flush hand and is unbeatable by any other combination. Eliminating identical hands that ignore relative suit values leaves 6,009,159 distinct 7-card hands. The number of distinct 5-card poker hands that are possible from 7 cards is 4,824. Perhaps surprisingly, this is fewer than the number of 5-card poker hands from 5 cards because some 5-card hands are impossible with 7 cards (e.g. There’s a seemingly endless list of nicknames used for hands in poker. The list seems to get bigger and bigger all the time too, as players are often coming up with new ones. Some of them are obvious, some of them amusing, and many of them are really quite tenuous. This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog - multiplication principle, permutation. 10) High Card – a hand in which no better hand was made (i.e., one in which each card is of a different rank than any other card and not all five are of the same suit or sequential in rank Poker games have many variations, some of which will be investigated here.
Poker traditionally has to be played with one deck. When you have more than one deck, the entire face of the game changes - more hands become possible, the probability of some hands changes drastically, and so on.
To demonstrate this, I decided to analyze poker with two decks of cards. As I calculate it, this is the correct ranking of hands:
Royal flush
Five of a kind
Straight flush
Flush with two pair
Four of a kind
Flush with one pair
Flush with no pairs (1)
Full house
Unflushed straight
Three of a kind
Two pair
One pair
High card
Note 1: You could, if you liked, join a flush with one pair and a flush with no pairs. Then, a full house would beat them. Flush with two pair is rare enough that it should stay separate, though.

 All ties are handled in the same way they would be in normal poker.
All ties are handled in the same way they would be in normal poker.Some notes:
- I tried to stick to the framework of basic poker hands as best I could. Because of this, five of a kind and flushes with pairs seemed like necessary additions. You could add all kinds of other spiffy hands if you wanted to (i.e. does having a suited pair make it better?), but that's beyond the point of my analysis.
- The Royal flush being top dog seemed like something players would expect, so I included it. If you preferred, you could consider the Royal to be a straight flush, with five of a kind being better. As long as the Royal flush is considered separately, however, it wins: there are 128 Royals and only 728 fives-of-a-kind.
- With five decks, the Royal flush gets dethroned as the best hand, because a flushed five of a kind (with only 52 possibilities) would be king. I'm not sure how adding more decks would affect this, however.
For the curious (and peer review), here are my actual calculations for each hand. 'C' means combinations, e.g. 8C3 is the number of combinations for drawing 3 items out of a list of 8, derived from the formula nCr = n! / ( (n-r)! * r! )
Edit: I forgot to account for flushed vs. unflushed pairs. Embarrassing! The new numbers are correct.
Royal flush:
4 different suits to flush in
2 different ways of getting each card in the royal flush
2
2
2
2
128 different Royal flushes
Five of a kind:
13 different ranks
8C5=56 different ways of getting five cards of that rank
728 different fives-of-a-kind
Straight flush:
4 different suits to flush in
9 different high cards (since Ace high gives royal flush)
2 different ways of getting each card in that particular straight flush
2
2
2
2
1172 different straight flushes
Flush with two pair:
4 different suits to flush in
13C2=78 combinations of ranks for pairs
11 different ranks for fifth card
1 combination for first pair in suit
1 combination for second pair in suit
2 cards possible for fifth card in given rank
6884 different flushes with two pair
Four of a kind:
13 different ranks for four-of-a-kind
12 different ranks for fifth card
8C4=70 combinations for four-of-a-kind
8 different cards of rank for fifth card
87360 different fours-of-a-kind
Flush with one pair:
4 different suits to flush in
13 different ranks for pair
12C3=220 combinations of ranks for extra cards
1 combination for pair
2 ways of getting each extra card in chosen rank and suit
2
2
91520 different flushes with one pair
Flush with no pairs:
4 different suits to flush in
13C5=1287 combinations of ranks for five cards
2 ways of getting each card in chosen rank and suit
2
2
2
2
164738 different flushes with no pairs, including straight flushes
Subtract 1172 straight flushes
163566 different flushes with no pairs or straight
Full house:
13 different ranks for three-of-a-kind
12 remaining ranks for pair
8C3=56 combinations for three-of-a-kind
8C2=28 combinations for pair
244608 different full houses
Unflushed straight:
10 different high cards for a straight
8 ways of getting each card in the straight
8
8
8
8
327680 different straights, including straight flushes
Subtract 1172 straight flushes
326508 different unflushed straights
Three of a kind:
13 different ranks for three-of-a-kind
12C2=66 combinations for ranks of extra cards
8C3=56 combinations for three-of-a-kind
8 different cards for fourth card
8 different cards for fifth card
3075072 different threes-of-a-kind
Unflushed two pair:
13C2=78 combinations of ranks for pairs
11 different ranks for fifth card

8C2=28 combinations for first pair
8C2=28 combinations for second pair
8 different cards of rank for remaining card
5381376 different hands with two pair
 Subtract 6884 different flushes with two pair
Subtract 6884 different flushes with two pair5374492 different unflushed hands with two pair
Unflushed pair:
13 different ranks for pair
12C3=220 combinations of ranks for extra cards
8C2=28 combinations for pair
8 different cards for each remaining extra card
8
8
41000960 different hands with one pair
Subtract 91520 different flushes with one pair
40909440 different unflushed hands with one pair
High card:
13C5=1287 combinations of ranks with no matches
Poker Hands What's Better Vegan
8 ways of getting each card8
8
8
8
42172416 different hands that do not contain a pair, three-of-a-kind, four-of-a-kind, or five-of-a-kind
Subtract 327680 different straights (including straight flushes)
Subtract 163566 different flushes with no pairs (not including straight flushes)
41681170 hands that contain no other hand
Poker Hands What's Better Hard
I was very bored today.
I'll say! This reminds me of some of the stuff that floats around the internet. It's entertaining, but always leaves me thinking 'Somebody has a lot of free time.'i.e. does having a suited pair make it better?
Yes.It's no different than the suited five of a kind in five deck poker that you mentioned.
Similarly, many Black Jack side bets pay X for specific cards, but pay more if they are suited.
i.e. does having a suited pair make it better?
Yes.It's no different than the suited five of a kind in five deck poker that you mentioned.
Similarly, many Black Jack side bets pay X for specific cards, but pay more if they are suited.
Poker Hands What's Better For You
Well, the flushed five of a kind is a special case: it's a flush, and it's five of a kind. Same with a straight flush (or for that matter, a Royal) in normal poker. You certainly could say that suited pairs are better, but keep in mind that there's a difference between, say, a suited pair of aces, and a flush with a pair of aces.Administrator
Three of a Kind
trips ..... combin(13,1)*combin(8,3) = 728
kickers ... combin(12,2)*combin(8,1)*combin(8,1) = 4224
total ..... 728 * 4224 = 3,075,072 (this agrees with your total)
Two Pair
pairs .... combin(13,2)*combin(8,2)*combin(8,2) = 61152
kicker ... combin(11,1)*combin(8,1) = 88
total .... 61152 * 88 = 5,381,376 (this is much higher than your total)
The above Two Pair figure does not subtract the counts for suited Two Pair hands if they are deemed to be higher in rank than other Two Pair hands. Nevertheless, the figures show that Three of a Kind is still a better-ranking hand than Two Pair.
I didn't check all of your figures, but I disagree with your Two Pair / Three of a Kind result:
Three of a Kind
trips ..... combin(13,1)*combin(8,3) = 728
kickers ... combin(12,2)*combin(8,1)*combin(8,1) = 4224
total ..... 728 * 4224 = 3,075,072 (this agrees with your total)
Two Pair
pairs .... combin(13,2)*combin(8,2)*combin(8,2) = 61152
kicker ... combin(11,1)*combin(8,1) = 88
total .... 61152 * 88 = 5,381,376 (this is much higher than your total)
The above Two Pair figure does not subtract the counts for suited Two Pair hands if they are deemed to be higher in rank than other Two Pair hands. Nevertheless, the figures show that Three of a Kind is still a better-ranking hand than Two Pair.
Yeah, that looks right. I'm not sure where my mistake was, but it seems to be in punching numbers into my calculator. How I made the exact same mistake more than once is a bit weird, but whatever. I'll change it.
Administrator
Yeah, that looks right. I'm not sure where my mistake was, but it seems to be in punching numbers into my calculator. How I made the exact same mistake more than once is a bit weird, but whatever. I'll change it.
I think you missed the last factor of 8, which corresponds to the suit of the kicker. You listed it, but forgot to include it in the calculation.Wizard
Administrator
The Casino I work at is getting a 6 deck Texas Hold'Em table game next month. 5 of a kind suited is the best hand. It's called Texas Shootout. It's reviewed on the Wizard of Odds site and looks pretty cool.
Here's the Wiz's page on it: http://wizardofodds.com/texasshootoutLooks kinda interesting.
Where do you work?
On a side note: Would that be advertising? Nah. I'd bet that the Wiz wouldn't want you to mention your casino in every post, but since this is tied to the thread's topic, I doubt he'd mind a quick plug.
This post works with 5-card Poker hands drawn from a standard deck of 52 cards. The discussion is mostly mathematical, using the Poker hands to illustrate counting techniques and calculation of probabilities
Working with poker hands is an excellent way to illustrate the counting techniques covered previously in this blog – multiplication principle, permutation and combination (also covered here). There are 2,598,960 many possible 5-card Poker hands. Thus the probability of obtaining any one specific hand is 1 in 2,598,960 (roughly 1 in 2.6 million). The probability of obtaining a given type of hands (e.g. three of a kind) is the number of possible hands for that type over 2,598,960. Thus this is primarily a counting exercise.
___________________________________________________________________________
Preliminary Calculation
Usually the order in which the cards are dealt is not important (except in the case of stud poker). Thus the following three examples point to the same poker hand. The only difference is the order in which the cards are dealt.
These are the same hand. Order is not important.
The number of possible 5-card poker hands would then be the same as the number of 5-element subsets of 52 objects. The following is the total number of 5-card poker hands drawn from a standard deck of 52 cards.
The notation is called the binomial coefficient and is pronounced “n choose r”, which is identical to the number of -element subsets of a set with objects. Other notations for are , and . Many calculators have a function for . Of course the calculation can also be done by definition by first calculating factorials.
Thus the probability of obtaining a specific hand (say, 2, 6, 10, K, A, all diamond) would be 1 in 2,598,960. If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of all diamond cards? It is
This is definitely a very rare event (less than 0.05% chance of happening). The numerator 1,287 is the number of hands consisting of all diamond cards, which is obtained by the following calculation.
The reasoning for the above calculation is that to draw a 5-card hand consisting of all diamond, we are drawing 5 cards from the 13 diamond cards and drawing zero cards from the other 39 cards. Since (there is only one way to draw nothing), is the number of hands with all diamonds.
If 5 cards are randomly drawn, what is the probability of getting a 5-card hand consisting of cards in one suit? The probability of getting all 5 cards in another suit (say heart) would also be 1287/2598960. So we have the following derivation.
Thus getting a hand with all cards in one suit is 4 times more likely than getting one with all diamond, but is still a rare event (with about a 0.2% chance of happening). Some of the higher ranked poker hands are in one suit but with additional strict requirements. They will be further discussed below.
Another example. What is the probability of obtaining a hand that has 3 diamonds and 2 hearts? The answer is 22308/2598960 = 0.008583433. The number of “3 diamond, 2 heart” hands is calculated as follows:
One theme that emerges is that the multiplication principle is behind the numerator of a poker hand probability. For example, we can think of the process to get a 5-card hand with 3 diamonds and 2 hearts in three steps. The first is to draw 3 cards from the 13 diamond cards, the second is to draw 2 cards from the 13 heart cards, and the third is to draw zero from the remaining 26 cards. The third step can be omitted since the number of ways of choosing zero is 1. In any case, the number of possible ways to carry out that 2-step (or 3-step) process is to multiply all the possibilities together.
___________________________________________________________________________
The Poker Hands
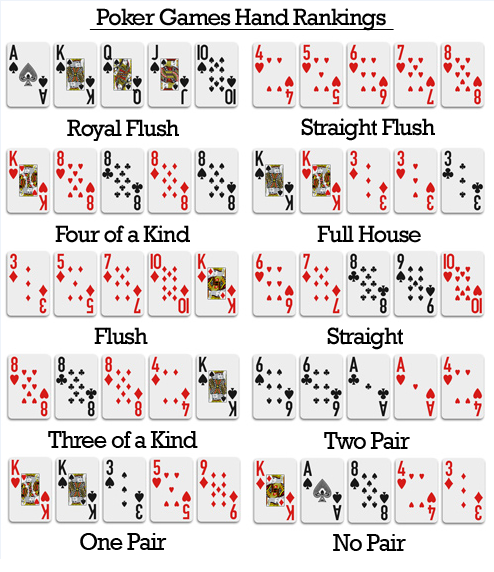
Here’s a ranking chart of the Poker hands.
The chart lists the rankings with an example for each ranking. The examples are a good reminder of the definitions. The highest ranking of them all is the royal flush, which consists of 5 consecutive cards in one suit with the highest card being Ace. There is only one such hand in each suit. Thus the chance for getting a royal flush is 4 in 2,598,960.
Royal flush is a specific example of a straight flush, which consists of 5 consecutive cards in one suit. There are 10 such hands in one suit. So there are 40 hands for straight flush in total. A flush is a hand with 5 cards in the same suit but not in consecutive order (or not in sequence). Thus the requirement for flush is considerably more relaxed than a straight flush. A straight is like a straight flush in that the 5 cards are in sequence but the 5 cards in a straight are not of the same suit. For a more in depth discussion on Poker hands, see the Wikipedia entry on Poker hands.
The counting for some of these hands is done in the next section. The definition of the hands can be inferred from the above chart. For the sake of completeness, the following table lists out the definition.
Definitions of Poker Hands
| Poker Hand | Definition | |
|---|---|---|
| 1 | Royal Flush | A, K, Q, J, 10, all in the same suit |
| 2 | Straight Flush | Five consecutive cards, |
| all in the same suit | ||
| 3 | Four of a Kind | Four cards of the same rank, |
| one card of another rank | ||
| 4 | Full House | Three of a kind with a pair |
| 5 | Flush | Five cards of the same suit, |
| not in consecutive order | ||
| 6 | Straight | Five consecutive cards, |
| not of the same suit | ||
| 7 | Three of a Kind | Three cards of the same rank, |
| 2 cards of two other ranks | ||
| 8 | Two Pair | Two cards of the same rank, |
| two cards of another rank, | ||
| one card of a third rank | ||
| 9 | One Pair | Three cards of the same rank, |
| 3 cards of three other ranks | ||
| 10 | High Card | If no one has any of the above hands, |
| the player with the highest card wins |
___________________________________________________________________________
Counting Poker Hands
Straight Flush
Counting from A-K-Q-J-10, K-Q-J-10-9, Q-J-10-9-8, …, 6-5-4-3-2 to 5-4-3-2-A, there are 10 hands that are in sequence in a given suit. So there are 40 straight flush hands all together.
Four of a Kind
There is only one way to have a four of a kind for a given rank. The fifth card can be any one of the remaining 48 cards. Thus there are 48 possibilities of a four of a kind in one rank. Thus there are 13 x 48 = 624 many four of a kind in total.
Full House
Let’s fix two ranks, say 2 and 8. How many ways can we have three of 2 and two of 8? We are choosing 3 cards out of the four 2’s and choosing 2 cards out of the four 8’s. That would be = 4 x 6 = 24. But the two ranks can be other ranks too. How many ways can we pick two ranks out of 13? That would be 13 x 12 = 156. So the total number of possibilities for Full House is
Note that the multiplication principle is at work here. When we pick two ranks, the number of ways is 13 x 12 = 156. Why did we not use = 78?
Flush
There are = 1,287 possible hands with all cards in the same suit. Recall that there are only 10 straight flush on a given suit. Thus of all the 5-card hands with all cards in a given suit, there are 1,287-10 = 1,277 hands that are not straight flush. Thus the total number of flush hands is 4 x 1277 = 5,108.
Straight
There are 10 five-consecutive sequences in 13 cards (as shown in the explanation for straight flush in this section). In each such sequence, there are 4 choices for each card (one for each suit). Thus the number of 5-card hands with 5 cards in sequence is . Then we need to subtract the number of straight flushes (40) from this number. Thus the number of straight is 10240 – 10 = 10,200.
Three of a Kind
There are 13 ranks (from A, K, …, to 2). We choose one of them to have 3 cards in that rank and two other ranks to have one card in each of those ranks. The following derivation reflects all the choosing in this process.
Two Pair and One Pair
These two are left as exercises.
High Card
The count is the complement that makes up 2,598,960.
The following table gives the counts of all the poker hands. The probability is the fraction of the 2,598,960 hands that meet the requirement of the type of hands in question. Note that royal flush is not listed. This is because it is included in the count for straight flush. Royal flush is omitted so that he counts add up to 2,598,960.
Probabilities of Poker Hands
| Poker Hand | Count | Probability | |
|---|---|---|---|
| 2 | Straight Flush | 40 | 0.0000154 |
| 3 | Four of a Kind | 624 | 0.0002401 |
| 4 | Full House | 3,744 | 0.0014406 |
| 5 | Flush | 5,108 | 0.0019654 |
| 6 | Straight | 10,200 | 0.0039246 |
| 7 | Three of a Kind | 54,912 | 0.0211285 |
| 8 | Two Pair | 123,552 | 0.0475390 |
| 9 | One Pair | 1,098,240 | 0.4225690 |
| 10 | High Card | 1,302,540 | 0.5011774 |
| Total | 2,598,960 | 1.0000000 |
___________________________________________________________________________
2017 – Dan Ma